1.简介
快速排序是经典的排序算法(所以也是经典面试题),采用了分治 (Divide-and-Conquer) 思想。
基本思想:通过一趟排序将要排序的数据分割成独立的两部分,其中一部分的所有数据都比另外一部分的所有数据都要小,
然后再按此方法对这两部分数据分别进行快速排序,整个排序过程可以递归进行,最终整个数据变成有序序列。
平均时间复杂度为O(nlogn),不需要额外的存储空间。
2.思路:
1) 在待排序数组a中 选一个基准(或者叫中轴,枢轴,英文pivot) pivot=a[i] , 将数组A划分成左右两部分 。
使i左边中的每个元素都小于pivot, i右边中每个元素都大于pivot;
2) 递归,解决分解后的两个数组;
3.示例图 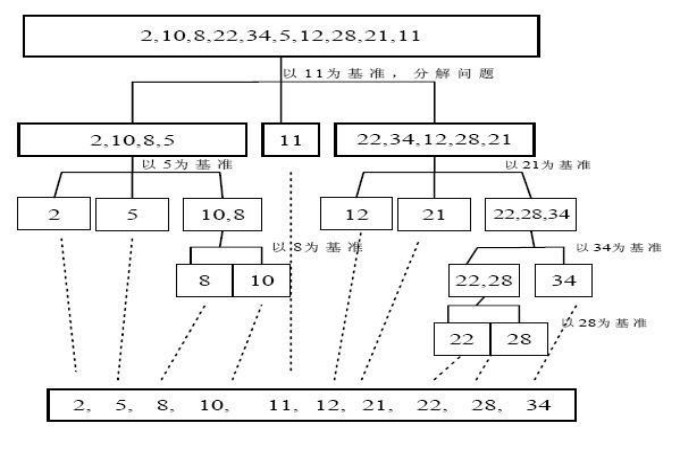
注:图片来源网络
4.代码实现
选取一个位置作为pivot枢轴,一般取整组记录的第一个数/最后一个,这里先选最后一个数为枢轴,后文详细说选取方法。
左指针从left向后走,直到找到一个大于pivot的值;右指针从right向前走,直至找到一个小于pivot的值,交换这两个数。
重复上一步一直进行下去,直到左右指针相遇,这时将pivot放到相遇的位置。
public static void quickSort(int[] arr, int left, int right) {
//只要子数组长度大于1就递归进行
if (left < right) {
//核心: 分成左右两部分
int p = partition(arr, left, right);
//递归
quickSort(arr, left, p - 1);
quickSort(arr, p + 1, right);
}
}
//以右边为基准
static int partition1(int[] arr, int left, int right) {
int pivot = arr[right];
int i = left, j = right;
while (i < j) {
while (arr[i] <= pivot && i < j) i++;
while (arr[j] >= pivot && i < j) j--;
swap(arr, i, j);
}
swap(arr, i, right);//此时i=j,用谁都行
return i;
}
//以左边为基准
static int partition2(int[] arr, int left, int right) {
int pivot = arr[left];
int i = left, j = right;
while (i < j) {
while (arr[j] >= pivot && i < j) j--; //思考:为何此处要j先移动?
while (arr[i] <= pivot && i < j) i++;
swap(arr, i, j);
}
swap(arr, left, i);//此时i=j
return i;
}
static void swap(int[] arr,int i, int j) {
int temp = arr[i];
arr[i] = arr[j];
arr[j]= temp;
}
5.快速排序的基准怎么选取?
一般可以随机找出一个数,也可以取固定位置,比如取中间的, 或者第一个或最后一个 作为基准.
如果这个值刚好是整段序列最大或者最小的值,那么这次划分就没意义了。
高级方法: 三数中值法
一组N个数的中值是第[N/2]个最大的数。基准的最好选择是数组的中值, 但是排完序才能看中值...所以只能近似
中值的估计量可以通过 随机选取三个元素 , 用它们的中值作为基准
一般的做法是使用左端、右端和中心位置上的三个元素的中值作为基准来近似
->无论以何种方式选取基准, 都可以将其与最右端的数交换, 增强代码通用性
static int partition3(int[] arr, int left, int right) {
// 1. 固定以右边第一个数为基准
// int pivot = arr[right];
// 2. 取数组中随机下标为基准, 将其与右边第一个数交换
// int random = new Random().nextInt(right - left) + left;
// Utils.swap(arr, random, right);
// int pivot = arr[right];
// 3.三数中值法
int m = left + (right - left) / 2; //数组中间元素的下标
if (arr[left]>arr[right])
swap(arr, left, right); //使左<右
if (arr[m] > arr[left])
swap(arr, m, left); //使左<中 ,现在左边最小,
if (arr[right] > arr[m] ) // 中间和右边比较, 较小的是中值
swap(arr, right, m); //使右<中,这样三个数中值就被放在右边了
int pivot = arr[right];
int i = left, j = right;
while (i < j) {
while (arr[i] <= pivot && i < j) i++;
while (arr[j] >= pivot && i < j) j--;
swap(arr, i, j);
}
swap(arr, j, right);
return i;
}6.优化
对于很小的数组,快速排序不如插入排序好, 因为快速排序是递归的。
通常的解决办法是不递归使用快速排序,而是对于小的数组使用插入排序(本文略)。
这种策略可以节省大约15%(相对于自始至终使用快速排序时)的运行时间。
一般可以取N=10,当然在5到20之间任一值都有可能是最好的选择
7.总结: 面试题:
写一下快速排序?
基准值怎么选? 三数中值.
怎么优化?小数组用插入排序.
初次发帖 水平有限 欢迎指正


